
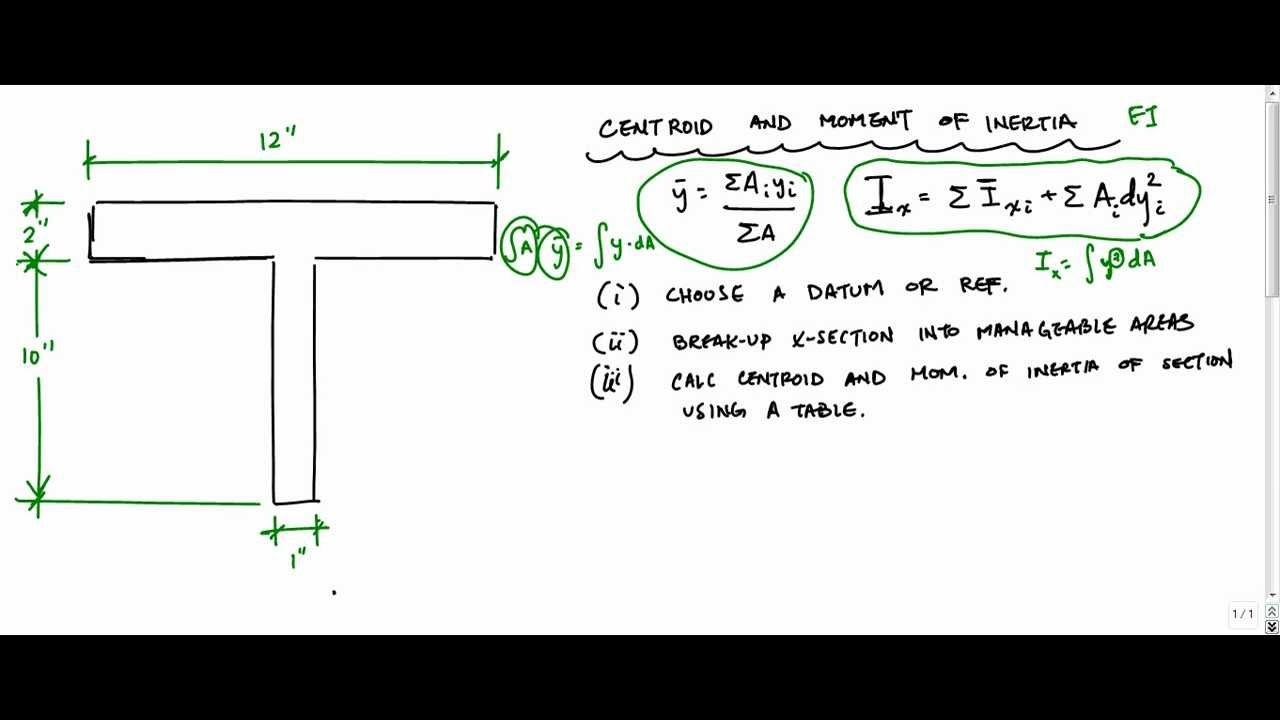
Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure. Radii of Gyration: The radii of gyration are. Where Ixy is the product of inertia, relative to centroidal axes x,y, and Ixy' is the product of inertia, relative to axes that are parallel to centroidal x,y ones, having offsets from them d_. The second moments of area / moments of inertia divided by these distances will equal the elastic section moduli. Compute the moment of inertia I of the cross- sectional area about the neutral axis. Where I' is the moment of inertia in respect to an arbitrary axis, I the moment of inertia in respect to a centroidal axis, parallel to the first one, d the distance between the two parallel axes and A the area of the shape (=bh in case of a rectangle).įor the product of inertia Ixy, the parallel axes theorem takes a similar form: The formulas for the section moduli of common cross sections are given. Moment of inertia Rectangular shape/section (formula) Strong Axis I y 1 12 h 3 w Weak Axis I z 1 12 h w 3 Dimensions of rectangular Cross-section. The moment of inertia must be specified with respect to a chosen axis of rotation.
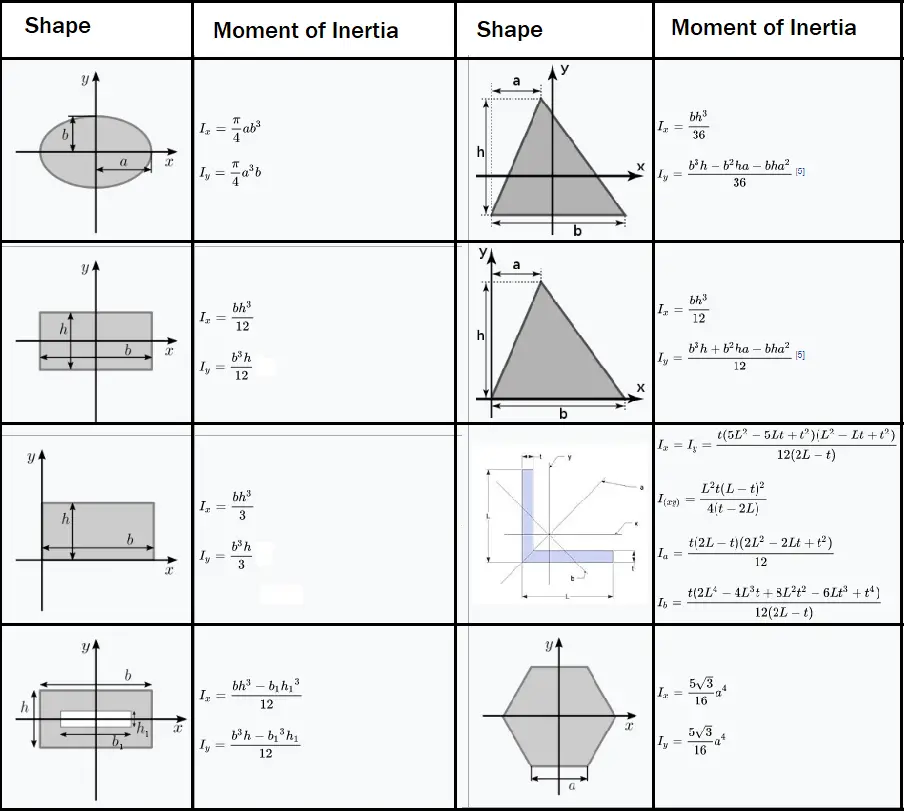
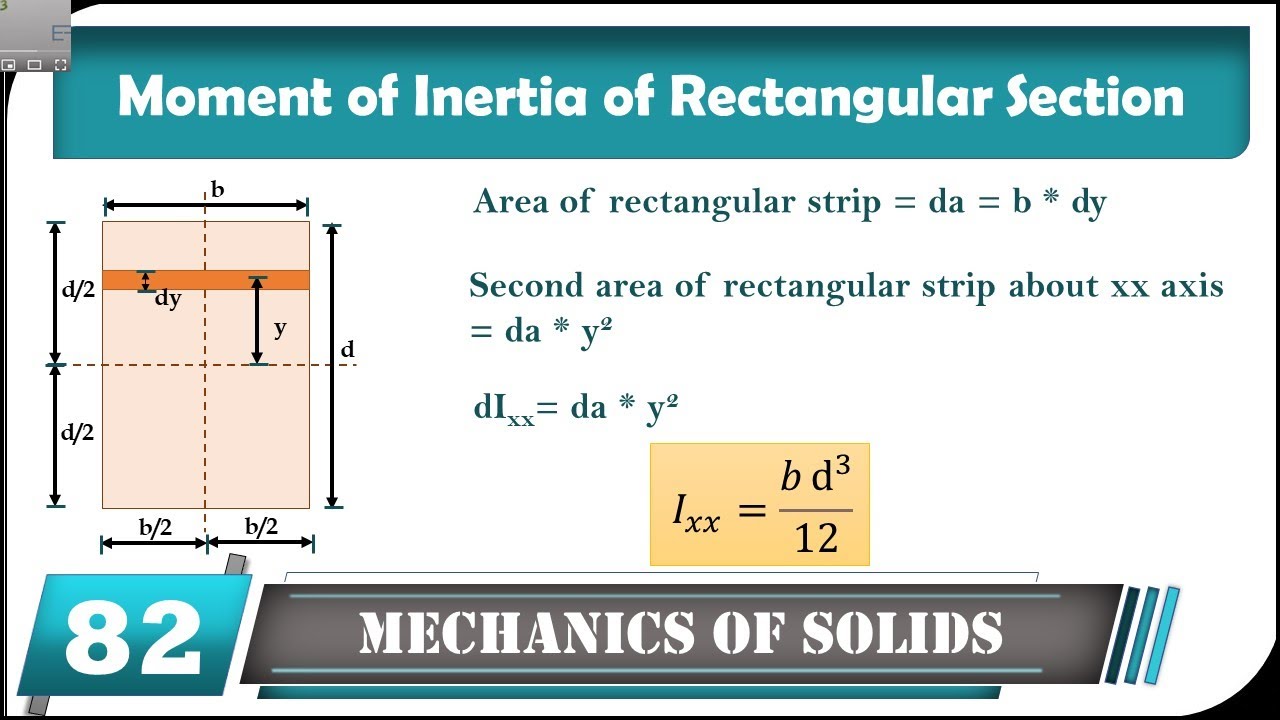

The so-called Parallel Axes Theorem is given by the following equation: Second Moment of Area Formula: T Section Area Moment of Inertia Formula Section properties of T-beam Equation Ixx bH(yc-H/2)2 + bH3/12 + hB(H + h/2 - yc)2. The moment of inertia of a tee section can be found, if the total area is divided into two, smaller ones, A, B, as shown in figure below. It appears in the relationships for the dynamics of rotational motion. Just as with centroids, each of these moments of. Since the first moment of area ‘QG’, calculated as the integral product of ‘yn’ and the infinitesimal area ‘dA’, is 0, the moment of inertia relative to the x-axis can be calculated as the sum of the moment of inertia ‘I’ and the product of ‘r2’ and cross-sectional area. Moments applied about the x x -axis and y y -axis represent bending moments, while moments about the z z - axis represent torsional moments. Figure 2: Parallel-Axis Theorem for Moment of Inertia. That is:Ī \ y_, the centroids of the two areas at either sides of the neutral axis can be found and the evaluation of the plastic modulus becomes straightforward.The moment of inertia of any shape, in respect to an arbitrary, non centroidal axis, can be found if its moment of inertia in respect to a centroidal axis, parallel to the first one, is known. 1: The moments of inertia for the cross section of a shape about each axis represents the shapes resistance to moments about that axis. To find its distance, y_c, from a convenient axis of reference, say the lower edge of the cross-section, the first moments of area, of the web and the two flanges, relative to the same edge are employed (note: the first moment of area is defined as the area times the distance of the area centroid from the axis of reference). The exact location of the centroid should be therefore calculated. The moments of inertia Iy and Iz are calculated with the parallel axis theorem the partial profiles of the cross-section are assumed to be perfectly connected. However, the same cannot be said for the other axis (x-x) since no symmetry exists around it, due to the unequal flanges. The clear height of the web, h_w that appears in above formulas, is the clear distance between the two flanges:ĭue to symmetry, around the y axis, the centroid of the cross-section must lie on the y axis too. The area A and the perimeter P of a double-tee, with unequal flanges, can be found by the next two formulas: It is the special area used in calculating stress in a beam cross-section during BENDING.


 0 kommentar(er)
0 kommentar(er)
